Question

Suppose the interest rate is 4.0 %. a. Having $ 200 today is equivalent to having what amount in one​ year? b. Having $ 200 in one year is equivalent to having what amount​ today? c. Which would you​ prefer, $ 200 today or $ 200 in one​ year? Does your answer depend on when you need the​ money? Why or why​ not? a. Having $ 200 today is equivalent to having what amount in one​ year? It is equivalent to ​$ nothing. ​(Round to the nearest​ cent.) b. Having $ 200 in one year is equivalent to having what amount​ today? It is equivalent to ​$ nothing. ​ (Round to the nearest​ cent.) c. Which would you​ prefer, $ 200 today or $ 200 in one​ year? Does your answer depend on when you need the​ money? Why or why​ not? ​"Because money today is worth more than money in the​ future, $ 200 today is preferred to $ 200 in one year. This answer is correct even if you​ don't need the money​ today, because by investing the $ 200 you receive today at the current interest​ rate, you will have more than $ 200 in one​ year." Is the above statement true or​ false? ▼ True False . ​(Select from the​ drop-down menu.)

Answer 1

(a) $200 today is equivalent to having $208 in one year with 4% interest rate.

(b) $192.31 today would be equivalent to $200 in one year with 4% interest rate.

(c) true

Step-by-step explanation:

(a) since simple interest is given as:

`I = (p* r* t)/(100)`

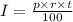
Where p = the principal amount

r = interest rate

t = number of years

Now, from the question our principal is $200 since we are to calculate the interest on it, and our rate is 4% as obvious from the question and as well as our time is 1year. Substituting these to the interest formula we get:

`I = (200* 4* 1)/(100)`

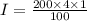
And that gives $8 as the interest, therefore in one year the amount we shall have will be: $200 + $8 = $208

(b) assuming we have 200 as the amount, we have now, we can get the principal we had last year at 4% interest with the following

`A = p(1 + (rt)/(100))`

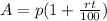
Now our amount is assumed to be $200 for 1year at 4% interest rate, therefore we have:

`$200 = p(1 + (4*1)/(100))`

This gives:

`$200 = p*1.04`

Which gives

`(200)/(1.04) = p`

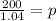
p = $192.31(to the nearest cents)

(c) The statement is obviously true, because the amount we buy things today are more expensive than the amount we bought them in previous years, so having $200 today is preferable because the interest on it is just so small and would be a waste of resources.