Question

The radius k of the equivalent hoop is called the radius of gyration of the given body. Using this formula, find the radius of gyration of (a) a cylinder of radius 1.20 m, (b) a thin spherical shell of radius 1.20 m, and (c) a solid sphere of radius 1.20 m, all rotating about their central axes.

Answer 1

Here is the full question:

The rotational inertia I of any given body of mass M about any given axis is equal to the rotational inertia of an equivalent hoop about that axis, if the hoop has the same mass M and a radius k given by:

`k=\sqrt{(I)/(M) }`

The radius k of the equivalent hoop is called the radius of gyration of the given body. Using this formula, find the radius of gyration of (a) a cylinder of radius 1.20 m, (b) a thin spherical shell of radius 1.20 m, and (c) a solid sphere of radius 1.20 m, all rotating about their central axes.

Answer:

a) 0.85 m

b) 0.98 m

c) 0.76 m

Step-by-step explanation:

Given that: the radius of gyration
`k=\sqrt{(I)/(M) }`

So, moment of rotational inertia (I) of a cylinder about it axis =
`(MR^2)/(2)`

`k=\sqrt{((MR^2)/(2))/(M) }`

`k=\sqrt{{(MR^2)/(2)}* (1)/(M) }`

`k=\sqrt{{(R^2)/(2)}`

`k={(R)/(√(2))`

`k={(1.20m)/(√(2))`

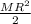
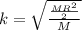
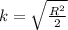
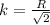
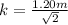
k = 0.8455 m

k ≅ 0.85 m

For the spherical shell of radius

(I) =
`(2)/(3)MR^2`

`k = \sqrt{((2)/(3)MR^2)/(M) }`

`k = \sqrt{(2)/(3) R^2}`

`k = \sqrt{(2)/(3) }*R`

`k = \sqrt{(2)/(3)} *1.20`

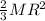
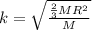
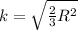
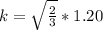
k = 0.9797 m

k ≅ 0.98 m

For the solid sphere of radius

(I) =
`(2)/(5)MR^2`

`k = \sqrt{((2)/(5)MR^2)/(M) }`

`k = \sqrt{(2)/(5) R^2}`

`k = \sqrt{(2)/(5) }*R`

`k = \sqrt{(2)/(5)} *1.20`

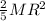
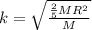
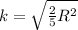
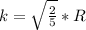
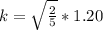
k = 0.7560

k ≅ 0.76 m