Question

Two ships leave a harbor at the same time. One ship travels on a bearing S 13 degrees W at 16 miles per hour. The other ship travels on a bearing N 75 degrees E at 11 miles per hour. How far apart will the ships be after 2 ​hours?

Answer 1

47 miles

Step-by-step explanation:

From the diagrammatic representation below;we can observe the illustration of the question.

after two hours;

The first ship = 16 miles per hour × 2 hours = 32 hours

the second ship = 11 miles per hour × 2 hours = 22 hours

to solve for ΔQPR in the diagram; we have;

∠ P = 13° + (2nd quadrant) + 15°

∠ P = 13° + 90° + 15°

∠ P = 118°

To solve for the distance apart the two ship, we can see from the diagram that it is "p". So, using cosine rule; we have:

p² = q² + r² - 2qr Cos P

p² = 22² + 32² - 2(22)(32) Cos 118°

p² = 484 + 1024 - (1408) (-0.4695)

p² = 1508 + 661.056

p² = 2169.056

p =
`√(2169.056)`

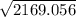
p = 46.5731252

p ≅ 47 miles

∴ The ships will be 47 miles far apart after 2 hours.