Answer:
29.04m/s
Step-by-step explanation:
Let the initial speed be u;
Since the motion of the stone is two-dimensional;
Let the horizontal component of the initial speed by
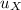 = u cos θ
= u cos θ
Let the vertical component of the initial speed by
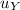 = u sin θ
= u sin θ
Where;
θ = the angle of projection above the horizontal.
Now using one of the equations of motion as follows, let us calculate the maximum height reached (from the top of the building) by the stone which is in the vertical component;
v² = u² + 2as -----------------(i)
Where;
v = vertical speed of the stone at maximum height = 0 [at maximum height, velocity is zero]
u = initial vertical speed of the stone =
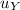 = u sin θ
= u sin θ
a = acceleration of the stone in the vertical direction = -g [ -ve sign shows that is upwards against acceleration due to gravity]
s = h = maximum height reached from the top of the building.
Therefore, equation (i) becomes;
0 = (
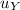 )² + 2(-g)h
)² + 2(-g)h
0 = (u sin θ)² - 2gh
=> 2gh = (u sin θ)²
=> h = (u sin θ)² / (2g) -----------------(ii)
From the question;
θ = 53°
u = 15m/s
Take g = 10m/s² and substitute other values into equation (ii) as follows;
h = (15 sin 53°)² / (2 x 10)
h = (15 x 0.7986)² / 20
h = 11.979² / 20
h = 143.496 / 20
h = 7.17m
Therefore, the maximum height reached from the top of the building is 7.17m.
However, the maximum height (H) reached from the bottom of the building (ground) is the sum of the height of the building (35m) and the further height reached (7.17m).
H = 35 + 7.17
H = 42.17m
Now, from the maximum height(H) let's calculate the speed of the rock as it hits the ground using equation (i) as follows;
v² = u² + 2as -------------------(ii)
Where;
v = speed of the stone as it hits the ground
u = initial velocity of the stone from maximum height = 0 [since velocity is 0 at maximum height]
a = acceleration due to gravity = +g [since the rock now moves downwards in the direction of gravity]
s = H = maximum height reached by the rock from the ground = 42.17m
Substitute these values into equation (ii) to get the speed (v) of the rock as it hits the ground;
v² = 0² + 2g(42.17) [Take g = 10m/s²]
v² = 0 + 2(10 x 42.17)
v² = 843.4
v =
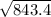
v = 29.04m/s
Therefore, the speed of the rock as it hits the ground is 29.04m/s