Question

You own a small storefront retail business and are interested in determining the average amount of money a typical customer spends per visit to your store. You take a random sample over the course of a month for 26 customers and find that the average dollar amount spent per transaction per customer is $77.506 with a standard deviation of $11.0714. When creating a 99% confidence interval for the true average dollar amount spend per customer, what is the margin of error

Answer 1

Explanation:

Hello!

The Confidence intervals for the population mean to follow the structure "point estimation"±" margin of error"

You as the store owner took a sample to determine the average amount of money a typical customer spends on your shop.

n= 26 customers.

X[bar]= $77.506

S= $11.0714

Assuming the variable X: the amount of money spent by a typical customer has a normal distribution and that there is no information about the population standard deviation, the best statistic to use for this estimation is a Students-t:

[X[bar] ±
`t_(n-1;1-\alpha /2)` *
`(S)/(√(n) )`]

`t_(n-1; 1-\alpha /2)= t_(25; 0.995)= 2.787`

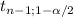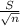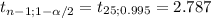
The margin of error of the interval is:

d=
`t_(n-1;1-\alpha /2)` *
`(S)/(√(n) )`

`d= 2.787 * (11.0714)/(√(26) )`

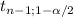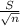
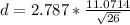
d= 6.051

I hope it helps!