Answer:
Explanation:
Hello!
The Confidence intervals for the population mean to follow the structure "point estimation"±" margin of error"
You as the store owner took a sample to determine the average amount of money a typical customer spends on your shop.
n= 26 customers.
X[bar]= $77.506
S= $11.0714
Assuming the variable X: the amount of money spent by a typical customer has a normal distribution and that there is no information about the population standard deviation, the best statistic to use for this estimation is a Students-t:
[X[bar] ±
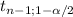 *
*
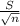 ]
]
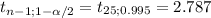
The margin of error of the interval is:
d=
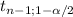 *
*
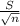
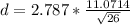
d= 6.051
I hope it helps!