Answer:
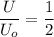
Step-by-step explanation:
Energy Stored in Capacitors
The capacitance of a parallel-plate capacitor is given by
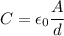
Where
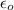 is the permitivity of the dielectric, A is the area of the plates and d is their separation. If the separation was doubled, the new capacitance would be
is the permitivity of the dielectric, A is the area of the plates and d is their separation. If the separation was doubled, the new capacitance would be
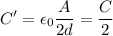
The energy stored in the initial condition is
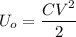
And the energy stored when the separation doubles is
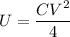
Thus the ratio
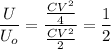
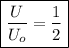
The energy is half the initial energy