Question

A parallel-plate capacitor is connected to a battery. The energy of the capacitor is U0U0U_0. The capacitor remains connected to the battery while the plates are slowly pulled apart until the plate separation doubles. The new energy of the capacitor is UUU. Find the ratio U/U0U/U0.

Answer 1

`\displaystyle (U)/(U_o)=(1)/(2)`

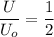
Step-by-step explanation:

Energy Stored in Capacitors

The capacitance of a parallel-plate capacitor is given by

`\displaystyle C=\epsilon_0(A)/(d)`

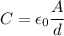
Where
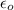`\epsilon_o` is the permitivity of the dielectric, A is the area of the plates and d is their separation. If the separation was doubled, the new capacitance would be

`\displaystyle C'=\epsilon_0(A)/(2d)=(C)/(2)`

The energy stored in the initial condition is

`\displaystyle U_o=(CV^2)/(2)`

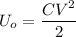
And the energy stored when the separation doubles is

`\displaystyle U=(CV^2)/(4)`

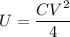
Thus the ratio

`\displaystyle (U)/(U_o)=((CV^2)/(4))/((CV^2)/(2))=(1)/(2)`

`\boxed{\displaystyle (U)/(U_o)=(1)/(2)}`

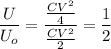
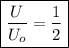
The energy is half the initial energy