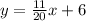Answer:
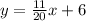
Explanation:
Given:
Two points are given
x = number of minutes
y = length of the lin
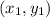 ⇒ (0, 6)
⇒ (0, 6)
 ⇒ (20, 17)
⇒ (20, 17)
We need to find the equation that represents the relationship between x, y.
Solution:
Using slope formula to find the slope of the equation of the line.
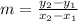
Substitute
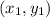 = (0, 6) and
= (0, 6) and
 = (20, 17) in above equation.
= (20, 17) in above equation.

So, slope of the line
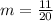
Using point slope formula.
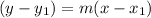 ------------(1)
------------(1)
Where, m = slope of the line
Substitute
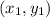 ⇒ (0, 6) and
⇒ (0, 6) and
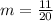 in equation 1.
in equation 1.
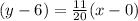

Add 6 both side of the equation.
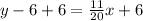
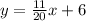
Therefore, the equation that represents the relationship between x and y is written as: