Answer:
52.39% probability that at least 10 cars in the sample have the defect.
Conditions:
Each car has only two possible outcomes. Either it is defective, or it is not. The cars are chosen at random, which means that the probability of a car being defective is independent from other cars. So we use the binomial probability distribution to solve this questions.
Explanation:
Conditions:
Each car has only two possible outcomes. Either it is defective, or it is not. The cars are chosen at random, which means that the probability of a car being defective is independent from other cars. So we use the binomial probability distribution to solve this questions.
We are working with a large sample, which means that we can approximate the binomial distribution to the normal.
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
Can be approximated to a normal distribution, using the expected value and the standard deviation.
The expected value of the binomial distribution is:
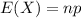
The standard deviation of the binomial distribution is:
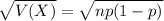
Normal probability distribution
Problems of normally distributed samples can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
When we are approximating a binomial distribution to a normal one, we have that
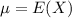 ,
,
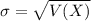 .
.
In this problem, we have that:
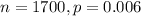
So
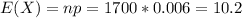
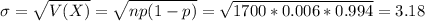
Approximate the probability that at least 10 cars in the sample have the defect.
This is 1 subtracted by the pvalue of Z when X = 10. So

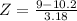

 has a pvalue of 0.4761.
has a pvalue of 0.4761.
1 - 0.4761 = 0.5239
52.39% probability that at least 10 cars in the sample have the defect.