Question

Select the correct answer from each drop-down menu.

CD is perpendicular to AB and passes through point C(5, 12).
If the coordinates of A and B are (-10, -3) and (7, 14), respectively, the x-intercept of CD is ______. The point ______ lies on CD.

Answer 1

x intercept of CD is (17, 0)

Point (-2, 19) lies on CD

Answer 2

x intercept of CD is (17, 0)

Point (-2, 19) lies on CD

Solution:

CD is perpendicular to AB and passes through point C(5, 12)

Coordinates of A and B are (-10, -3) and (7, 14)

Find slope of AB

`m = (y_2-y_1)/(x_2-x_1)`

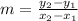
From given,

`(x_1, y_1) = (-10 , -3)\\\\(x_2, y_2) = (7, 14)`

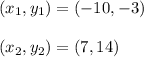
Substituting we get,

`m = (14+3)/(7+10)\\\\m = (17)/(17)\\\\m = 1`

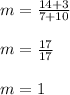
CD is perpendicular to AB

We know that,

Product of slope of AB and slope of line CD which is perpendicular to AB is equal to -1

Therefore,

`1 * \text{ slope of CD } = -1\\\\\text{ slope of CD } = -1`

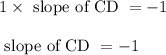
The equation of CD in slope intercept form is:

y = mx + c --------- eqn 1

Where,

m is the slope

c is the y intercept

Substitute m = -1 and (x, y) = (5, 12) in eqn 1

12 = -1(5) + c

c = 12 + 5

c = 17

Substitute m = -1 and c = 17 in eqn 1

y = -x + 17 ------ eqn 2

The x-intercept is found by setting y equal to 0

0 = -x + 17

x = 17

Thus x intercept of CD is (17, 0)

For the second part, we just plug in the different points and see if the equation is true:

Substitute (x, y) = (-5, 24) in eqn 2

`(-5, 24)\rightarrow 24=-(-5)+17\rightarrow 24=5+17\rightarrow 24=22\\\\(doesn't work)\\\\(-2, 19)\rightarrow 19=-(-2)+17\\\\\rightarrow 19=2+17\\\\\rightarrow 19=19`

Thus, Point (-2, 19) lies on CD