Question

An aircraft component is fabricated from an aluminum alloy that has a plane-strain fracture toughness of 40 MPa1m (36.4 ksi1in.). It has been determined that fracture results at a stress of 300 MPa (43,500 psi) when the maximum (or critical) internal crack length is 4.0 mm (0.16 in.). For this same component and alloy, will fracture occur at a stress level of 260 MPa (38,000 psi) when the maximum internal crack length is 6.0 mm (0.24 in.)? Why or why not?

Answer 1

`Y = (40 Mpa √(m))/(300 Mpa √(\pi 0.002m))= 1.682`

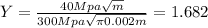
Now we can solve for the fracture level with this formula:

`\sigma_F = (K_(lc))/(Y √(\pi d_x))`

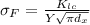
We can use the parameter of Y from the previous equation since this value not changes.

`d_x = 6/2 = 3 mm =0.003m`

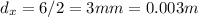
And replacing we have:

`\sigma_F= (40 Mpa √(m))/(1.682 √(\pi 0.003m))= 244.96 Mpa`

And for this case we see that this value not correspond to 260 Mpa the value reported, so then the correct answer for this case would be 244.96 Mpa for the new crack length of 6mm = 0.006 m

Step-by-step explanation:

We need to solve for the parameter Y given by this expression:

`Y = (K_(lc))/(\sigma √(\pi d))`

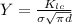
Where:

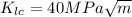`K_(lc) = 40 MPa √(m)` represent the fracture toughness

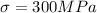`\sigma = 300 MPa` represent the stress level

`d = (4 mm)/(2)= 2mm = 0.002 m`

And if we replace we got:

`Y = (40 Mpa √(m))/(300 Mpa √(\pi 0.002m))= 1.682`

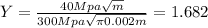
Now we can solve for the fracture level with this formula:

`\sigma_F = (K_(lc))/(Y √(\pi d_x))`

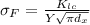
We can use the parameter of Y from the previous equation since this value not changes.

`d_x = 6/2 = 3 mm =0.003m`

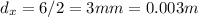
And replacing we have:

`\sigma_F= (40 Mpa √(m))/(1.682 √(\pi 0.003m))= 244.96 Mpa`

And for this case we see that this value not correspond to 260 Mpa the value reported, so then the correct answer for this case would be 244.96 Mpa for the new crack length of 6mm = 0.006 m