Question

If a particle moving in a circular path of radius 5 m has a velocity function v = 4t2 m/s, what is the magnitude of its total acceleration at t = 1 s?

Answer 1

8.62m/s²

Step-by-step explanation:

The total acceleration (a) of a particle undergoing a circular motion is given by the vector sum of the tangential acceleration (
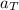`a_(T)`) and the centripetal or radial acceleration (
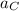`a_(C)`) of the particle. The magnitude of this total acceleration is given as follows;

a =
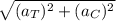`\sqrt{(a_(T) )^2 + (a_(C) )^2}` ------------------(i)

(i) But;

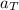`a_(T)` = time rate of change of velocity (v) = Δv / Δt =
`(dv)/(dt)`

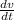
From the question,

v = 4t² -------------------(ii)

Therefore, differentiating equation (ii) with respect to t gives the tangential acceleration as follows;

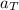`a_(T)` = dv / dt =
`(dv)/(dt)` =
`(d(4t^(2) ))/(dt)`

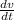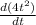
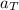`a_(T)` = 8t

Now, at time t = 1s, the tangential acceleration is given by substituting t = 1 into equation (iii) as follows;

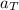`a_(T)` = 8(1)

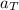`a_(T)` = 8m/s²

(ii) Also;

`a_(C)` =
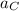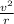`(v^2)/(r)` ------------------------ (iv)

Where;

r = radius of the circular path of motion = 5m

v = velocity of motion = 4t²

Substitute these values into equation (iv) as follows;

`a_(C)` =
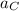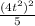`((4t^2)^2)/(5)` -------------------------------(v)

Now, at time t = 1s, the centripetal acceleration is given by substituting t = 1 into equation (v) as follows;

`a_(C)` =
`((4(1)^2)^2)/(5)`

`a_(C)` =
`((4)^2)/(5)`

`a_(C)` =
`(16)/(5)`

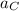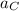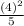
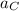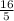
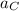`a_(C)` = 3.2m/s²

(iii) Now substitute the values of
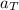`a_(T)` and
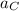`a_(C)` into equation (i) as follows;

a =
`√((8)^2 + (3.2)^2)`

a =
`√((64) + (10.24))`

a =
`√(74.24)`

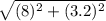
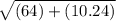
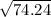
a = 8.62 m/s²

Therefore, the magnitude of the total acceleration at t = 1s is 8.62m/s²

Answer 2

8.62m/s²

Step-by-step explanation:

the particle is experiencing both translational and circular motion

v=4t²

`a_(t)`=
`(dv)/(dt)`=8t

at t=1s,
`(dv)/(dt)`=8(1)=8m/s²

`a_(c)` =
`(v^(2) )/(r)`

at t=1, v= 4(1)² = 4m/s

`a_(c)`=4²/5

`a_(c)`=3.2m/s²

∴ magnitude of total acceleration, a

a=
`\sqrt{a_(t) ^(2) + a_(c) {2} }`

a=
`\sqrt{8^(2) +3.2^(2) }`

a=
`√(64+10.24)`

a=
`√(74.24)`

a=8.62m/s²