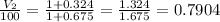 is the volume of the sample when the water content is 10%.
is the volume of the sample when the water content is 10%.
Step-by-step explanation:
Given Data:
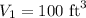
First has a natural water content of 25% =
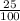 = 0.25
= 0.25
Shrinkage limit,
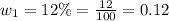
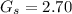
We need to determine the volume of the sample when the water content is 10% (0.10). As we know,
![V \propto[1+e]](https://img.qammunity.org/2021/formulas/engineering/college/dumde1dobrdwkhncgver2onswouf285z14.png)
 ------> eq 1
------> eq 1

The above equation is at
 ,
,
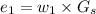
Applying the given values, we get

Shrinkage limit is lowest water content
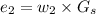
Applying the given values, we get
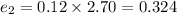
Applying the found values in eq 1, we get