Question

Which expression 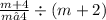is equivalent to StartFraction m minus 4 Over m + 4 EndFraction divided by (m + 2) ?

StartFraction m minus 4 Over (m + 4) (m + 2) EndFraction
StartFraction (m + 4) (m + 2) Over m minus 4 EndFraction
StartFraction (m minus 4) (m + 2) Over m + 4 EndFraction
StartFraction m + 4 Over (m minus 4) (m + 2) EndFraction

Answer 1

A: m-4/(m+4)(m+2)

Explanation:

Used symbolab.

Answer 2

Expression
`(m+4)/(m−4) /(m+2)` is equivalent to
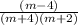`((m - 4) )/((m + 4) (m + 2))`. So, Option A is the right choice.

To answer this question, we can use the following steps:

Rewrite the division as multiplication by the reciprocal.

`(m-4)/(m+4) / (m+2) = (m-4)/(m+4) * (1)/(m+2)`

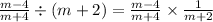
Multiply the two numerators and multiply the two denominators.

`(m-4)/(m+4) * (1)/(m+2) = \frac{(m-4) * 1} {(m+4) * (m+2)}`

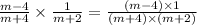
Simplify the expression.

`\frac{(m-4) * 1} {(m+4) * (m+2)} = (m-4)/(m^2+6m+8)`

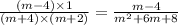
Therefore, the only expression that is equivalent to
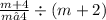`(m+4)/(m−4) /(m+2)` is:
`(m-4)/(m^2+6m+8)`

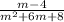
So the answer is:
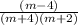`((m - 4) )/((m + 4) (m + 2))` Option A is the right choice.