Question

A company selling glass ornaments by​ mail-order expects, from previous​ history, that 8​% of the ornaments it ships will break in shipping. You purchase two ornaments as gifts and have them shipped separately to two different addresses. What is the probability that both arrive​ safely? What did you​ assume?

Answer 1

`P(X=2) =(2C2) (0.92)^2 (1-0.92)^(2-2)= 0.8464`

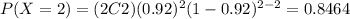
And we assume that the probability of succes on this case (no break) is 1-0.08=0.92 and we also assume that the events (packages sent) are independent

Explanation:

Previous concepts

The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".

Solution to the problem

Let X the random variable of interest, on this case we now that:

`X \sim Binom(n=2, p=1-0.08=0.92)`

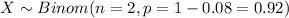
The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x)`

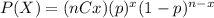
Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

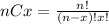
And for this case we want to calculate the probability that both arrive safely so we want to find:

`P(X=2)`

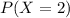
Using the probability mass function we have this:

`P(X=2) =(2C2) (0.92)^2 (1-0.92)^(2-2)= 0.8464`

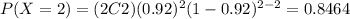
And we assume that the probability of succes on this case (no break) is 1-0.08=0.92 and we also assume that the events (packages) are independent