Question

Suppose you want to find the sum of two sinusoidal voltages, given as follows: v1(t)=V1 cos(ωt+ϕ1) and v2(t)=V2 cos(ωt+ϕ2)v1(t)=V1 cos(ωt+ϕ1) and v2(t)=V2 cos(ωt+ϕ2).

If you stay in the time domain, you will have to use trigonometric identities to perform the addition. But if you transform to the frequency domain, you can simply add the phasors V1V1 and V2V2 as complex numbers using your calculator. Your answer will be a phasor, so you will need to inverse phasor-transform it to get the answer in the time domain. This is an example of a problem that is easier to solve in the frequency domain than in the time domain.

Use phasor techniques to find an expression for v(t) expressed as a single cosine function, where v(t)=[100cos(300t+45∘)+500cos(300t−60∘)] V. Enter your expression using the cosine function. Round real numbers using two digits after the decimal point. Any angles used should be in degrees.

Answer 1

Rectangular form V = 320.71 - j362.3

Polar form V = 483.85 < -48.48°

Phasor form V = 483.85cos(300t - 48.48°)

Step-by-step explanation:

We are given a sinusoidal function

V(t) = 100cos(300t + 45°) + 500cos(300t - 60°)

We are required to find the v(t) expressed as a single cosine function using phasor technique.

In polar form,

100cos(300t + 45°) = 100 < 45°

500cos(300t - 60°) = 500 < -60°

In rectangular form,

100 < 45° = 70.71 + j70.71

500 < -60° = 250 - j433.01

Adding the two signals

(70.71 + j70.71) + (250 - j433.01)

In rectangular form,

V = 320.71 - j362.3

In polar form

V = 483.85 < -48.48°

Therefore, the answer is

in rectangular form V = 320.71 - j362.3

in polar form V = 483.85 < -48.48°

in phasor form V = 483.85cos(300t - 48.48°)

Conversion from Rectangular to Polar form:

V = X + jY to Magnitude < Angle

V = 320.71 - j362.3

Magnitude =
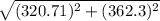`√((320.71)^2 +(362.3)^2)` = 483.85

Angle = tan⁻¹(Y/X) = tan⁻¹(-362.3/320.71) = -48.48°

V = 483.85 < -48.48°

Conversion from Polar to Rectangular form:

V = 483.85 < -48.48°

X = Magnitude*cos(Angle) and jY = Magnitude*sin(Angle)

X = 483.85*cos(-48.48°) and jY = 483.85*sin(-48.48°)

X = 320.71 and jY = -362.3

V = 320.71 - j362.3

Answer 2

Attached is the full solution.