Question

A capacitor is made from two hollow, coaxial, iron cylinders, one inside the other. The inner cylinder is negatively charged and the outer is positively charged; the magnitude of the charge on each is 15.5 pC. The inner cylinder has a radius of 0.600 mm, the outer one has a radius of 5.20 mm, and the length of each cylinder is 25.0 cm.

(a) What is the capacitance?
(b) What applied potential difference is necessary to produce these charges on the cylinders?

Answer 1

(a). The capacitance is
`6.43*10^(-12)\ F`

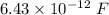
(b). The potential difference is necessary to produce these charges on the cylinders are 2.41 V.

Step-by-step explanation:

Given that,

Charge = 15.5 pC

Inner Radius = 0.600 mm

Outer radius = 5.20 mm

Length = 25.0 cm

(a). We need to calculate the capacitance

Using formula of capacitor

`C=(2\pi\epsilon_(0)l)/(ln(b)/(a))`

Put the value into the formula

`C=(2\pi*8.85*10^(-12)*25.0*10^(-2))/(ln(5.20)/(0.600))`

`C=6.43*10^(-12)\ F`

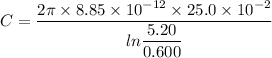
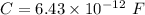
The capacitance is
`6.43*10^(-12)\ F`

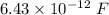
(b). We need to calculate the potential difference is necessary to produce these charges on the cylinders

Using formula of charge

`q=CV`

`V=(q)/(C)`

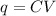
Put the value into the formula

`V=(15.5*10^(-12))/(6.43*10^(-12))`

`V=2.41\ V`

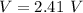
Hence, (a). The capacitance is
`6.43*10^(-12)\ F`

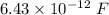
(b). The potential difference is necessary to produce these charges on the cylinders are 2.41 V.