Question

The conventional coal-fired power plant has an efficiency of about 33%. Assuming that all the coal in Example 8–3 were used to generate electricity (it was not), estimate the time until exhaustion, if the efficiency were raised to 40

Answer 1

T = 385.2 years ... constant rate of consumption

T = 44.707 years ... 5.15% increase per year in average consumption

Step-by-step explanation:

Solution:

- Obtain the value of consumption rate fromm Example 8-3.

Consumption Rate = 128.5 EJ / year

- The efficiency of coal fired power plant was raised to 40%:

A = efficiency * consumption rate

A = 0.40*128.5

A = 51.4 EJ /year

- For the case demand D = 19,800 EJ remains constant and international consumption at C = 120.8 EJ, the time to exhaustion would be:

Time = D / A

= 19,800 EJ / 51.4 EJ /year

= 385.2 years

- For average consumption of coal based increased at R = 5.15% per year, the reserves will last according to growth expression as follows:

`D = C*((1 + (R)/(100))^t - 1 )/((R)/(100))`

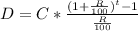
- Solve for time t:

R*[D/100*C] + 1 = ( 1 + 0.01*R)^t

Ln | R*[D/100*C] + 1 | = t*Ln | 1 + 0.01*R |

t = Ln | R*[D/100*C] + 1 | / Ln | 1 + 0.01*R |

t = Ln | 0.0515*[19,800/120.8] + 1 | / Ln | 1 + 0.0515 |

t = 44.707 years