Answer:
The total charge on the sphere is 46.11 x 10⁻³ C
Step-by-step explanation:
Given:
charge density of innermost section, σ = −5.0C/m³
radius of the innermost section, r = 6.0cm
charge density of the outer layer ,σ = +8.0 C/m³
radius of the outer layer, r =12.0cm
volume of sphere is given as
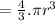
Charge enclosed by the innermost section = volume x charge density
volume
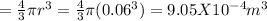
Enclosed charge, q₁ = −5.0C/m³ X 9.05 x 10⁻⁴ m³
= - 4.53 x 10⁻³ C
Charge at the outer surface
Volume =
![(4)/(3)\pi [r_2{^3} - r_1{^3}] = (4)/(3)\pi [0.12{^3} - 0.06{^3}] = 0.00633 {m^3}](https://img.qammunity.org/2021/formulas/physics/college/9tmyy3zgvwzlyxjpxfz1x3cqgey7rdalg6.png)
Enclosed charge, q₂ = +8.0 C/m³ X 0.00633 m³
= 50.64 x 10⁻³ C
Total charge on the sphere; Q = q₁ + q₂
= - 4.53 x 10⁻³ C + 50.64 x 10⁻³ C
= 46.11 x 10⁻³ C
Therefore, the total charge on the sphere is 46.11 x 10⁻³ C