Question

A nonconducting sphere is made of two layers. The innermost section has a radius of 6.0 cm and a uniform charge density of −5.0C/m^3. The outer layer has a uniform charge density of +8.0C/m^3 and extends from an inner radius of 6.0 cm to an outer radius of 12.0 cm. Find the total charge Q on the sphere.

Answer 1

The total charge Q on the nonconducting sphere is 0.0132C.

Step-by-step explanation:

The total charge Q on the nonconducting sphere can be found by calculating the charge on each layer and adding them together. To find the charge on the innermost section, we multiply the charge density (-5.0C/m^3) by the volume of the section, which is (4/3)π(0.06m)^3. This gives us -0.09C. Similarly, the charge on the outer layer can be found by multiplying the charge density (+8.0C/m^3) by the volume of the section, which is 4/3π((0.12m)^3 - (0.06m)^3). This gives us 0.1032C. Therefore, the total charge Q on the sphere is -0.09C + 0.1032C = 0.0132C.

Answer 2

The total charge on the sphere is 46.11 x 10⁻³ C

Step-by-step explanation:

Given:

charge density of innermost section, σ = −5.0C/m³

radius of the innermost section, r = 6.0cm

charge density of the outer layer ,σ = +8.0 C/m³

radius of the outer layer, r =12.0cm

volume of sphere is given as
`= (4)/(3).\pi r^3`

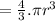
Charge enclosed by the innermost section = volume x charge density

volume
`= (4)/(3)\pi r^3 = (4)/(3)\pi (0.06^3) = 9.05 X 10^(-4) m^3`

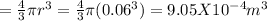
Enclosed charge, q₁ = −5.0C/m³ X 9.05 x 10⁻⁴ m³

= - 4.53 x 10⁻³ C

Charge at the outer surface

Volume =
`(4)/(3)\pi [r_2{^3} - r_1{^3}] = (4)/(3)\pi [0.12{^3} - 0.06{^3}] = 0.00633 {m^3}`

Enclosed charge, q₂ = +8.0 C/m³ X 0.00633 m³

= 50.64 x 10⁻³ C

Total charge on the sphere; Q = q₁ + q₂

= - 4.53 x 10⁻³ C + 50.64 x 10⁻³ C

= 46.11 x 10⁻³ C

Therefore, the total charge on the sphere is 46.11 x 10⁻³ C