Answer:
There is not enough evidence to claim that Alaska has a lower proportion of identity theft.
Explanation:
In this case, we have a population proportion for the identity theft complaints, that is 0.23.
In Alaska, we have a sample proportion of
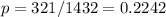
We have to test the hypothesis to know if the claim that Alaska has a lower proportion than the population has evidence.
The null and alternative hypothesis are:
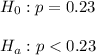
The level of significance level depends on which error we want to minimize.
The Type I error is when we reject the null hypothesis although it is true.
The Type II error is when we don't reject the null hypothesis even when it is false.
As we want to know if there is enough evidence that the alternative hypothesis is true, we want to minimize the Type I error. To do so, we have to decrease the level of significance.
We choose a level of significance of 0.01.
The estimated standard deviation is calculated as:
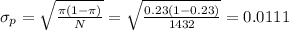
The statistic z can be calculated as:
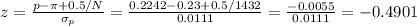
The P-valueof z=-0.4901 is P=0.312.
The P-value is greater then the level of significance, so the effect is not statistically significant. (NOTE: even raising the level of significance to alpha=0.1, the effect is not significant)
There is not enough evidence to claim that Alaska has a lower proportion of identity theft.