Question

According to the February 2008 Federal Trade Commission report on consumer fraud and identity theft, 23% of all complaints in 2007 were for identity theft. In that year, Alaska had 321 complaints of identity theft out of 1,432 consumer complaints ("Consumer fraud and," 2008). Does this data provide enough evidence to show that Alaska had a lower proportion of identity theft than 23%? State the type I and type II errors in this case, consequences of each error type for this situation, and the appropriate alpha level to use. According to the February 2008 Federal Trade Commission report on consumer fraud and identity theft, 23% of all complaints in 2007 were for identity theft. In that year, Alaska had 321 complaints of identity theft out of 1,432 consumer complaints ("Consumer fraud and," 2008). Does this data provide enough evidence to show that Alaska had a lower proportion of identity theft than 23%?

Answer 1

There is not enough evidence to claim that Alaska has a lower proportion of identity theft.

Explanation:

In this case, we have a population proportion for the identity theft complaints, that is 0.23.

In Alaska, we have a sample proportion of

`p=321/1432=0.2242`

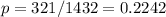
We have to test the hypothesis to know if the claim that Alaska has a lower proportion than the population has evidence.

The null and alternative hypothesis are:

`H_0: p=0.23\\\\H_a:p<0.23`

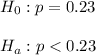
The level of significance level depends on which error we want to minimize.

The Type I error is when we reject the null hypothesis although it is true.

The Type II error is when we don't reject the null hypothesis even when it is false.

As we want to know if there is enough evidence that the alternative hypothesis is true, we want to minimize the Type I error. To do so, we have to decrease the level of significance.

We choose a level of significance of 0.01.

The estimated standard deviation is calculated as:

`\sigma_p=\sqrt{(\pi(1-\pi))/(N) } =\sqrt{(0.23(1-0.23))/(1432) } =0.0111`

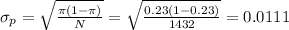
The statistic z can be calculated as:

`z=(p-\pi+0.5/N)/(\sigma_p) =(0.2242-0.23+0.5/1432)/(0.0111)=(-0.0055)/(0.0111)=-0.4901`

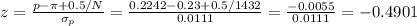
The P-valueof z=-0.4901 is P=0.312.

The P-value is greater then the level of significance, so the effect is not statistically significant. (NOTE: even raising the level of significance to alpha=0.1, the effect is not significant)

There is not enough evidence to claim that Alaska has a lower proportion of identity theft.