Answer:
(a) Quiz 1: mean 1 (μ1) =
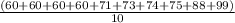 = 72
= 72
Quiz 2: mean 2(μ2) =
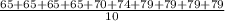 = 72
= 72
Quiz 3: μ3=
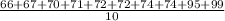 = 76
= 76
Quiz 4: μ4 =
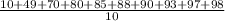 = 76
= 76
Quiz 1: median1 = 72
Quiz 2: median2 = 72
Quiz 3: median3 = 72
Quiz 4: median4 = 86.5
Quiz 1: mode1 = 60
Quiz 2: mode2= 65 and 79
Quiz 3: mode3 = 72 and 74
Quiz 4: mode4 = 0
(b) Mean and median agree with each other but mode doesn't, because, although all are measures of the "average", mean is the "real" average because it uses each data to fidn itself; median is the central value of the data, so sometimes it matches the mean. The mode, however, is related to the frequency of "appearance", in other words, how often the number repeates itself in the data set, so more than often, it doesn't agree with the others.
(c) For the mean, the strength or advantage is that it can be calculated in any given circunstance (continuous or discrete) and which better represents the average of a set. The disavantages or weakness is that it can be influenciated by other values;
The advantage of both median and mode is that it's not affected by outliers (data different from the rest). In the case of median, it can give more information about the set. Their disavantage is that they don't yield on statistical manipulation.
Related to mode, it can be difficult to interpret the data because the distribution can be bimodal or multi-modal.
(d) To be symmetrical or skewed, you can compare mean and median. But, if the distribution is multi-modal, the interpretation can be different.
In quiz 1, the mean and median are the same, so the data is symmetric.
In quiz 2 and quiz 3, the data show a bimodal distribution. As the frequency of each number are the same, both data are symmetric.
In quiz 4, the mean is less than the median. This means it skewed to the left.
(e) Comparing quizzes 1, 2 and 3, the students were more or less even, in other words, they were in the same level, which were demonstrated in the mean. In the 4th Friday, due to the difference among the numbers, the median increase drastically but the mean kept almost the same.