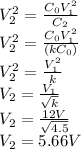Answer:
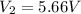
Step-by-step explanation:
The electrical energy stored in the empty capacitor is defined as:
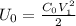
Where
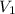 is the potential difference across the plates of the capacitor and
is the potential difference across the plates of the capacitor and
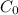 is its capacitance.
is its capacitance.
The capacitance of the capacitor with a dielectric is given by:
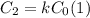
The electrical energy stored in the capacitor filled with a dielectric is:
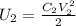
We have
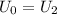 . Thus:
. Thus:
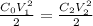
Replacing (1) and solving for
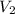 :
: