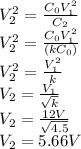Question

What must be the potential difference across the plates of the capacitor filled with a dielectric so that it stores the same amount of electrical energy as the empty capacitor?

Answer 1

`V_2=5.66V`

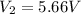
Step-by-step explanation:

The electrical energy stored in the empty capacitor is defined as:

`U_0=(C_0V_1^2)/(2)`

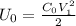
Where
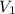`V_1` is the potential difference across the plates of the capacitor and
`C_0` is its capacitance.

The capacitance of the capacitor with a dielectric is given by:

`C_2=kC_0(1)`

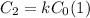
The electrical energy stored in the capacitor filled with a dielectric is:

`U_2=(C_2V_2^2)/(2)`

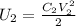
We have
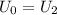`U_0=U_2`. Thus:

`(C_0V_1^2)/(2)=(C_2V_2^2)/(2)`

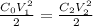
Replacing (1) and solving for
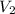`V_2`:

`V_2^2=(C_0V_1^2)/(C_2)\\V_2^2=(C_0V_1^2)/((kC_0))\\V_2^2=(V_1^2)/(k)\\V_2=(V_1)/(√(k))\\V_2=(12V)/(√(4.5))\\V_2=5.66V`