Option C:
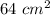 is the area of the composite figure.
is the area of the composite figure.
Step-by-step explanation:
It is given that the composite figure is divided into two congruent trapezoids.
The measurements of both the trapezoids are
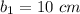
 and
and
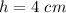
Area of the trapezoid =
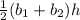
Substituting the values, we get,
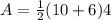
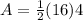
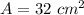
Thus, the area of one trapezoid is
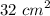
The area of the composite figure can be determined by adding the area of the two trapezoids.
Thus, we have,
Area of the composite figure = Area of the trapezoid + Area of the trapezoid.
Area of the composite figure =
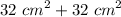
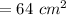
Thus, the area of the composite figure is
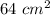
Hence, Option C is the correct answer.