Question

Given that the random variable X is normally distributed with a mean of 80 and a standard deviation of 10, P(85 X 90) is a. 0.3413 b. 0.1498 c. 0.5328 d. 0.1915

Answer 1

The answer is b.) 0.1498

Explanation:

The normal distribution of a random variable, x, is said to have a mean,
`\mu` = 80 and a standard deviation,
`\sigma` = 10.

We have to find the probability of P(85 < x < 90) .

We first find the Z values which represent the x variable by using the formula Z =
`(x - \mu)/(\sigma)`.

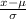Thus we can write

P( 85 < x < 90)

= P(
`((85 - 80))/(10) < Z < ((90 - 80))/(10)`)

= P(0.5 < Z < 1)

= P(Z < 1) - P(Z < 0.5).

When we are asked to probabilities between two values we can separate them into two probabilities and find their difference to give the answer as shown above.

From the Z - tables we can calculate P(Z < 0.5) = 0.6915 and P(Z < 1) = 0.8413

Therefore P( 85 < x < 90) = 0.8413 - 0.6915 = 0.1498.

The answer is b.) 0.1498