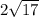Question

__
What is √68 in simplest radical form?

Answer 1

The simplest radical form is
`2 √(17)`

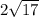
Step-by-step explanation:

The expression is
`√(68)`

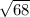
To determine the radical form, let us write the number 68 as a product of prime factors.

Thus, we have,

`√(68) =√(2*2*17)`

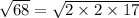
Since, 2, 17 are prime factors and hence, no further factorization is possible.

Hence, it can be written as,

`√(68) =\sqrt{2^(2) *17}`

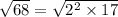
Applying the radical rule
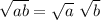`√(a b)=√(a) \ √(b)`, we have,

`√(68) =\sqrt{2^(2)} √(17)`

Simplifying, we have,

`√(68) =2 √(17)`

Thus, the simplest radical form is
`2 √(17)`