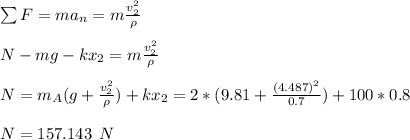Question

A 2-kg ball B is traveling horizontally at 10 m/s when it strikes 2-kg ball A. Ball A is initially at rest and is attached to a spring with constant 100 N/m and an unstretched length of 1.2 m. Knowing the coefficient of restitution between A and B is 0.8 and friction between all surfaces is negligible, determine the normal force between A and the ground when it is at the bottom of the hill.

Answer 1

`N=157.143\:\:N`

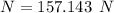
Step-by-step explanation:

We firstly determine the impulse momentum of ball B in tangential direction.

`m_B v_0_f=m_B v_B_t\\\\v_B_t=v_0_f=10\sin(40^\circ)=6.428\:\:m/s`

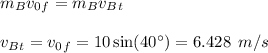
Then we simplify the equation for impulse momentum for ball A and ball B.

`m_B v_0 = m_A v_A + m_B v_B_x + m_B v_B_t\\\\2*10=2v_A+2[v_B_n\cos(40^\circ)+6.428\sin(40^\circ)]\\\\2v_A+1.532v_B_n=11.736`

Now the equation for coefficient of restitution is determined to solve above equation with 2 equations 2 unknowns.

`v_B_n-v_A_n=e(0-v_0_n)\\\\v_B_n-v_A\cos(40^\circ)=-0.8*10cos(40^\circ)\\\\v_B_n-0.776v_A=-6.128`

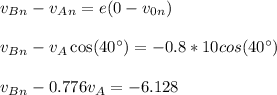
Hence,

`v_A=6.655\:\:m/s\\\\v_B_n=-1.03\:\:m/s`

Now we apply Conservation of Energy Principle.

`T_1+V_1=T_2+V_2\\\\(1)/(2) m_Av_A^2+0=(1)/(2) m_Av_2^2+m_Agh_2+(1)/(2) kx_2^2\\\\h_2=-0.4\:\:m, \:\:thus, \:\:x_2=1.2-0.4=0.8\:\:m\\\\(1)/(2) *2*(6.655)^2=(1)/(2) *2v_2^2+2*9.81*(-0.4)+(1)/(2) *100*(0.8)^2\\\\44.289=v_2^2-7.848+32\\\\v_2=4.487\:\:m/s`

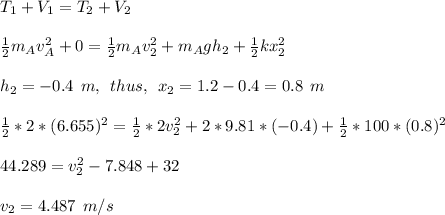
Finally, we apply Newton's 2nd Law.

`\sum F=ma_n=m(v_2^2)/(\rho)\\\\N-mg-kx_2=m(v_2^2)/(\rho)\\\\N=m_A(g+(v_2^2)/(\rho)})+kx_2=2*(9.81+((4.487)^2)/(0.7))+100*0.8\\\\N=157.143\:\:N`