Question

The Ceiling Tile Game:

11% of the time that we point up randomly, the ceiling tile we're pointing to is cracked. Suppose we point three times. Let X be the number of cracked ceiling tiles we get. The probability distribution for X is (exact answers, no rounding):
X probability
0- ?
1-?
2-?
3-?
The mean of X is (exact answer) -?
The standard deviation of X is (to three places after the decimal) -?
If we play "The Ceiling Tile Game" 1700 times, the total number of cracked ceiling tiles should be about (exact answer) -?

Answer 1

Explanation:

in this case, x = the number of success in 3 trials, so x is a binomial distributed random variable, hence:

P(x=0) = (3C0)*(0.11)^0*(1-0.11)^(3-0)=0.704969

P(x=1) = (3C1)*(0.11)^1*(1-0.11)^(3-1) = 0.261393

P(x=2) = (3C2)*(0.11)^2*(1-0.11)^(3-2)= 0.032307

P(x=3) = (3C3)*(0.11)^3*(1-0.11)^(3-3)= 0.001331

E(x) = n*p = 3*0.11=0.33

σ =
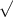`\sqrt{}`(n*p*(1-p)=0.542

E(y) = n*p = 1700*0.11=187