Question

Consider the decomposition of the compound C5H6O3 as follows: C5H6O3(g)  C2H6(g) + 3CO(g) A 5.63 g sample of pure C5H6O3(g) was placed in an evacuated 2.50 L flask and heated to 200.ºC. At equilibrium, the pressure in the flask was 1.63 atm. Calculate K for this reaction.

Answer 1

`K_(eq)=1.02x10^(-4)`

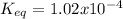
Step-by-step explanation:

Hello,

In this case, the first step is to compute the initial moles of C₅H₆O₃ as shown below:

`5.63gC_5H_5O_3*(1molC_5H_5O_3)/(114gC_5H_5O_3)=0.0494molC_5H_5O_3`

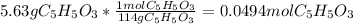
After that, by knowing that the final pressure is 1.63 atm, one computes the total moles at the equilibrium as follows:

`n_(total)^(eq)=(P_(total)^(eq)V)/(RT)=(1.63atm*2.50L)/(0.082(atm*L)/(mol*K)*473.15K) =0.105mol`

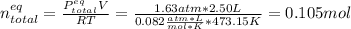
Then, by knowing the moles at the equilibrium considering the change "
`x`", which yields to:

`\ \ \ \ \ C_5H_6O_3(g) \leftrightarrow C_2H_6(g) + 3CO(g)\\I\ \ \ \ \ 0.0494mol\ \ \ \ \ \ 0mol \ \ \ \ \ \ \ \ 0mol\\C\ \ \ \ \ \ -x\ \ \ \ \ \ \ \ \ \ \ \ \ x\ \ \ \ \ \ \ \ \ \ \ \ \ \ 3x\\E\ \ 0.0494mol-x\ \ \ \ x\ \ \ \ \ \ \ \ \ \ \ \ \ 3x`

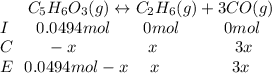
The total moles at the equilibrium turn out:

`n_(total)^(eq)=0.0494mol-x+x+3x`

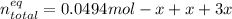
By solving for "
`x`", we've got:

`3x=0.105mol-0.0494mol\\x=(0.0556mol)/(3)\\x=0.0185mol`

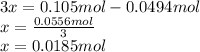
Finally, the equilibrium constant is:

`K_(eq)=((x)(3x)^3)/(0.0494-x)=((0.0185mol)(3*0.0185mol)^3)/(0.0494mol-0.0185mol)=1.02x10^(-4)`

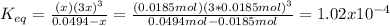
Best regards.