Question

Allison is in the business of manufacturing phones. She must pay a daily fixed cost to rent the building and equipment, and also pays a cost per phone produced for materials and labor. The daily fixed costs are $400 and and the total cost of producing 3 phones in a day would be $550. Write an equation for the function C ( p ) , C(p), representing total cost, in dollars, of producing p p phones in a given day.

Answer 1

Oranges

Explanation:

Ryan is in the business of manufacturing phones. He must pay a daily fixed cost to rent the building and equipment, and also pays a cost per phone produced for materials and labor. The equation C=300+50pC=300+50p can be used to determine the total cost, in dollars, of producing pp phones in a given day. What is the yy-intercept of the equation and what is its interpretation in the context of the problem?

Answer 2

`C(p)=50p+400`

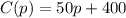
Explanation:

Let p represent number of phones produced in one day.

We have been given that Allison must pay a daily fixed cost to rent the building and equipment, and also pays a cost per phone produced for materials and labor. The daily fixed costs are $400 and and the total cost of producing 3 phones in a day would be $550.

Let x represent cost of each phone.

We can represent this information in an equation by equating total cost of 3 phones with 550 as:

`3x+400=550`

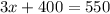
Let us find cost of each phone.

`3x=550-400`

`3x=150`

`x=(150)/(3)`

`x=50`

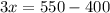
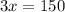
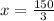
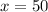
Since cost of each phone is $50, so cost of p phones would be
`50p`.

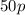The total cost would be equal to cost of p phones plus fixed cost.

`C(p)=50p+400`

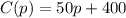
Therefore, our required cost function would be
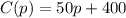`C(p)=50p+400`.