Answer:
The equations are missing but we can solve the problem from the given information
The equation
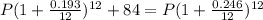 can be used to solve for the principal P for which the cards offer the same deal over the course of a year
can be used to solve for the principal P for which the cards offer the same deal over the course of a year
Explanation:
The formula of the compounded interest is
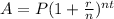 , where
, where
- A is the future value of the investment/loan, including interest
- P is the principal investment amount
- r is the annual interest rate (decimal)
- n is the number of times that interest is compounded per unit t
- t is the time the money is invested or borrowed for
Card A:
∵ Credit card A has an APR of 19.3% and an annual fee of $84
∴ r = 19.3% = 19.3 ÷ 100 = 0.193
∴ Annual fee = 84
∵ Interest is compounded monthly for a year
∴ n = 12 and t = 1
- Substitute the values of r, n and t in the formula above
∴
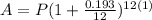
- Add the value of the annual fee
∴
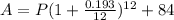
Card B:
∵ Credit card B has an APR of 24.6% and no annual fee
∴ r = 24.6% = 24.6 ÷ 100 = 0.246
∴ Annual fee = 0
∵ Interest is compounded monthly for a year
∴ n = 12 and t = 1
- Substitute the values of r, n and t in the formula above
∴
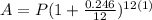
∴
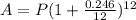
- Equate The equations of cards A and B
∴
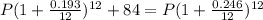
The equation
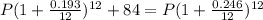 can be used to solve for the principal P for which the cards offer the same deal over the course of a year
can be used to solve for the principal P for which the cards offer the same deal over the course of a year