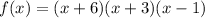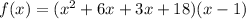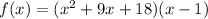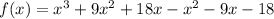Question

The function f(x) is a cubic function and the zeros of f(x) are -6, -3 and 1. Assume the leading coefficient of f(x) is 1. Write the equation of the cubic polynomial in standard form.

Answer 1

`f(x)=x^3+8x^2+9x-18`

Explanation:

If
`c` is a zero of
`f`, then
`x-c` is a factor of
`f`.

Since -6,-3, and 1 are zeros, then we have the following factors of
`f`:

`(x-(-6))`,
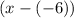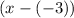`(x-(-3))`, and
`(x-1)`.

Let's put it together.

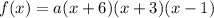`f(x)=a(x+6)(x+3)(x-1)`, where
`a` is the leading coefficient and we are given to make it equal to 1, has zeros -6,-3, and 1.

We now need to put the factored form of
`f` into standard form by using multiplication and combining of like terms.

`f(x)=(x+6)(x+3)(x-1)`

`f(x)=(x^2+6x+3x+18)(x-1)`

`f(x)=(x^2+9x+18)(x-1)`

`f(x)=x^3+9x^2+18x-x^2-9x-18`

`f(x)=x^3+8x^2+9x-18`

Answer 2

f(x) = x³+8x²+9x-18

Explanation:

Factors are: (x+6)(x+3)(x-1)

= (x+6)(x²+3x-x-3)

= (x+6)(x²+2x-3)

= x³+2x²-3x+6x²+12x-18

f(x) = x³+8x²+9x-18