Answer: x = 11
==============================================
Work Shown:
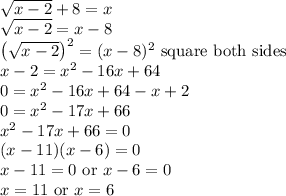
Those are the two possible solutions . We need to check each possible solution.
Plug in x = 11 then simplify. If we get the same number on both sides, then x = 11 is confirmed.
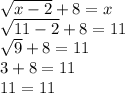
We get 11 on both sides, so the solution x = 11 is confirmed.
Repeat for x = 6 as well
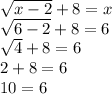
We do not get the same thing on both sides, so x = 6 is not a solution. We consider this extraneous.