Question

Solve for the sqrt(x-2)+8=x

Answer 1

Answer: x = 11

==============================================

Work Shown:

`√(x-2)+8=x\\√(x-2)=x-8\\\left(√(x-2)\right)^2=(x-8)^2 \text{ square both sides}\\x-2=x^2-16x+64\\0=x^2-16x+64-x+2\\0=x^2-17x+66\\x^2-17x+66 = 0\\(x-11)(x-6) = 0\\x-11 = 0 \text{ or } x-6 = 0\\x = 11 \text{ or } x = 6\\`

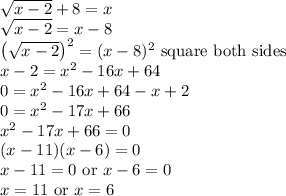
Those are the two possible solutions . We need to check each possible solution.

Plug in x = 11 then simplify. If we get the same number on both sides, then x = 11 is confirmed.

`√(x-2)+8=x\\√(11-2)+8=11\\√(9)+8=11\\3+8=11\\11=11\\`

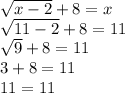
We get 11 on both sides, so the solution x = 11 is confirmed.

Repeat for x = 6 as well

`√(x-2)+8=x\\√(6-2)+8=6\\√(4)+8=6\\2+8=6\\10=6\\`

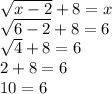
We do not get the same thing on both sides, so x = 6 is not a solution. We consider this extraneous.