Question

Suppose the function f has an initial value of 1,000 and a decay rate of 5%. Let the function g have an initial value of 400 and increase at a growth rate of 17%. Estimate a value of x, to the nearest tenth, for which f(x) = g(x).

Answer 1

4.4 years

Explanation:

cuz maths

Answer 2

4.4 years

Explanation:

we know that

The equation of a exponential decay function is given by

`y=a(1-r)^x`

where

a is the initial value

r is the rate of change

The equation of a exponential growth function is given by

`y=a(1+r)^x`

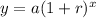
where

a is the initial value

r is the rate of change

step 1

Find f(x)

in this problem we have

`f(x)=1,000(1-0.05)^x`

`f(x)=1,000(0.95)^x`

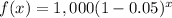
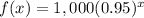
step 2

Find g(x)

in this problem we have

`g(x)=400(1+0.17)^x`

`g(x)=400(1.17)^x`

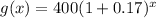
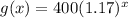
step 3

we have

`f(x)=1,000(0.95)^x`

`g(x)=400(1.17)^x`

`f(x)=g(x)`

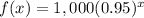
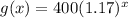
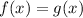
solve the system by graphing

The solution is the x-coordinate of intersection point

using a graphing tool

The solution is x=4.4 years

see the attached figure