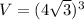Answer:
The volume of cube C is

Explanation:
step 1
Find the diameter of sphere B
we know that
When a cube is inscribed in a sphere, the long diagonal of the cube is a diameter of the sphere
Let
L ----> the length side of cube A
d ----> the diagonal of the base of cube A
D ---> the long diagonal of cube A
Find the diagonal of the base of cube A
Applying the Pythagorean Theorem
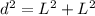
we have
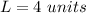
substitute
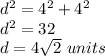
Find the long diagonal of cube A
Applying the Pythagorean Theorem

substitute
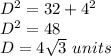
step 2
we know that
If sphere B is inscribed in cube C, then the length side of cube C is equal to the diameter of sphere B
Let
c ----> the length side of cube C
we have that
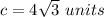
The volume of cube C is equal to
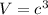
substitute