Answer:
(a) The rate of change of blood pressure with respect to 50 pounds weight level is 0.26mm/pound. (To the nearest hundredth)
(b) The rate of change of blood pressure with respect to 80 pounds weight level is 0.16mm/pound. (To the nearest hundredth)
Explanation:
The formula relating weight and blood pressure is given by:
P(x) = 12.9(9 + lnx) for
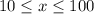
The rate of change of one thing with respect to the other is the derivative of the first with respect to the second. Therefore, for the purpose of this question, the rate of change of blood pressure P(x) with respect to the weight (x) is the derivative of P(x) with x.
Rate of change =
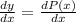
Differentiating the equation given with respect to x i.e
P(x) = 12.9(9 + lnx)
expanding the bracket by multiplying the characters in the bracket with the character outside the bracket, we have:
P(x) = 12.9 x 9 + 12.9 x lnx
P(x) = 116.1 + 12.9lnx,
differentiating this P(x), Recall from standard derivative,
 of a constant is zero
of a constant is zero
 of lnx is
of lnx is
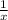
Applying this to the P(x) with x

= 0 +
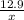
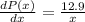
(a) When weight x = 50 pounds,
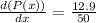 = 0.258
= 0.258
= 0.26mm/pound (To the nearest hundredth)
(b) When weight x = 80 pounds,
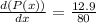 = 0.16125
= 0.16125
= 0.16mm/pound (To the nearest hundredth)
From our result, it is shown that the rate of change of blood pressure with respect to weight reduces with increase in weight.