Answer:
a.
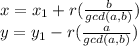
b. x = -8 and y = 4
Step-by-step explanation:
This question is incomplete. I will type the complete question below before giving my solution.
For integers a, b, c, consider the linear Diophantine equation
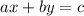
Suppose integers x0 and yo satisfy the equation; that is,
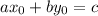
what other values
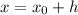 and
and
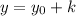
also satisfy ax + by = c? Formulate a conjecture that answers this question.
Devise some numerical examples to ground your exploration. For example, 6(-3) + 15*2 = 12.
Can you find other integers x and y such that 6x + 15y = 12?
How many other pairs of integers x and y can you find ?
Can you find infinitely many other solutions?
From the Extended Euclidean Algorithm, given any integers a and b, integers s and t can be found such that
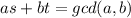
the numbers s and t are not unique, but you only need one pair. Once s and t are found, since we are assuming that gcd(a,b) divides c, there exists an integer k such that gcd(a,b)k = c.
Multiplying as + bt = gcd(a,b) through by k you get
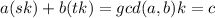
So this gives one solution, with x = sk and y = tk.
Now assuming that ax1 + by1 = c is a solution, and ax + by = c is some other solution. Taking the difference between the two, we get
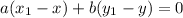
Therefore,
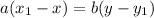
This means that a divides b(y−y1), and therefore a/gcd(a,b) divides y−y1. Hence,
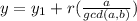 for some integer r. Substituting into the equation
for some integer r. Substituting into the equation
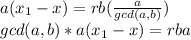
or
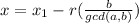
Thus if ax1 + by1 = c is any solution, then all solutions are of the form
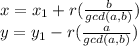
In order to find all integer solutions to 6x + 15y = 12
we first use the Euclidean algorithm to find gcd(15,6); the parenthetical equation is how we will use this equality after we complete the computation.
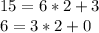
Therefore gcd(6,15) = 3. Since 3|12, the equation has integral solutions.
We then find a way of representing 3 as a linear combination of 6 and 15, using the Euclidean algorithm computation and the equalities, we have,
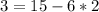
Because 4 multiplies 3 to give 12, we multiply by 4
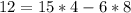
So one solution is
 &
&
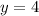
All other solutions will have the form
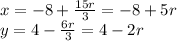
where
 ∈ Ζ
∈ Ζ
Hence by putting r values, we get many (x, y)