Question

For integers a, b, and c, consider the linear Diophantine equation ax C by D c: Suppose integers x0 and y0 satisfy the equation; that is, ax0 C by0 D c. What other values x D x0 C h and y D y0 C k also satisfy ax Cby D c?

Answer 1

For a linear Diophantine equation, if integers x0 and y0 satisfy the equation, we can find other values x and y that also satisfy the equation by using the formula x = x0 + h and y = y0 + k, where h and k are any integers.

Step-by-step explanation:

For a linear Diophantine equation of the form ax + by = c, if integers x0 and y0 satisfy the equation (ax0 + by0 = c), then we can find other values x and y that also satisfy the equation.

To find these values, we can use the formula x = x0 + h and y = y0 + k, where h and k are any integers.

By substituting these values into the equation, we get (a(x0 + h) + b(y0 + k) = c). When we expand and simplify the equation, we still get the same value c, showing that these new values x and y also satisfy the linear Diophantine equation.

Answer 2

a.

`x = x_1+r((b)/(gcd(a, b)) )\\y=y_1-r((a)/(gcd(a, b)) )`

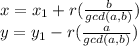
b. x = -8 and y = 4

Step-by-step explanation:

This question is incomplete. I will type the complete question below before giving my solution.

For integers a, b, c, consider the linear Diophantine equation

`ax+by=c`

Suppose integers x0 and yo satisfy the equation; that is,

`ax_0+by_0 = c`

what other values

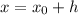`x = x_0+h` and
`y=y_0+k`

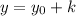
also satisfy ax + by = c? Formulate a conjecture that answers this question.

Devise some numerical examples to ground your exploration. For example, 6(-3) + 15*2 = 12.

Can you find other integers x and y such that 6x + 15y = 12?

How many other pairs of integers x and y can you find ?

Can you find infinitely many other solutions?

From the Extended Euclidean Algorithm, given any integers a and b, integers s and t can be found such that

`as+bt=gcd(a,b)`

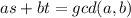
the numbers s and t are not unique, but you only need one pair. Once s and t are found, since we are assuming that gcd(a,b) divides c, there exists an integer k such that gcd(a,b)k = c.

Multiplying as + bt = gcd(a,b) through by k you get

`a(sk) + b(tk) = gcd(a,b)k = c`

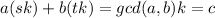
So this gives one solution, with x = sk and y = tk.

Now assuming that ax1 + by1 = c is a solution, and ax + by = c is some other solution. Taking the difference between the two, we get

`a(x_1-x) + b(y_1-y)=0`

Therefore,

`a(x_1-x) = b(y-y_1)`

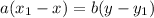
This means that a divides b(y−y1), and therefore a/gcd(a,b) divides y−y1. Hence,

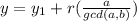`y = y_1+r((a)/(gcd(a, b)))` for some integer r. Substituting into the equation

`a(x_1-x)=rb((a)/(gcd(a, b)) )\\gcd(a, b)*a(x_1-x)=rba`

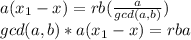
or

`x = x_1-r((b)/(gcd(a, b)) )`

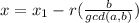
Thus if ax1 + by1 = c is any solution, then all solutions are of the form

`x = x_1+r((b)/(gcd(a, b)) )\\y=y_1-r((a)/(gcd(a, b)) )`

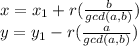
In order to find all integer solutions to 6x + 15y = 12

we first use the Euclidean algorithm to find gcd(15,6); the parenthetical equation is how we will use this equality after we complete the computation.

`15 = 6*2+3\\6=3*2+0`

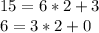
Therefore gcd(6,15) = 3. Since 3|12, the equation has integral solutions.

We then find a way of representing 3 as a linear combination of 6 and 15, using the Euclidean algorithm computation and the equalities, we have,

`3 = 15-6*2`

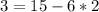
Because 4 multiplies 3 to give 12, we multiply by 4

`12 = 15*4-6*8`

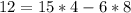
So one solution is

`x=-8` &
`y = 4`

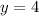
All other solutions will have the form

`x=-8+(15r)/(3) = -8+5r\\y=4-(6r)/(3) =4-2r`

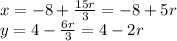
where
`r` ∈ Ζ

Hence by putting r values, we get many (x, y)