Answer:
Part 2: The probability of X≤2 or X≥4 is 0.5.
Part 3: The value of marginal probability of y is
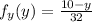 for
for
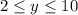
Part 4:The value of E(y) is 4.6667.
Part 5:The value of
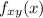 is
is
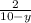 for
for
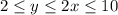
Part 6:The value of
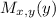 is
is

Part 7:The value of E(x) is 3.6667.
Part 8:The value of E(x,y) is 36.
Part 9:The value of Cov(x,y) is 18.8886.
Part 10:X and Y are not independent variables as

Explanation:
As the complete question is here, however some of the values are not readable, thus the question is found online and is attached herewith.
From the given data, the joint distribution is given as
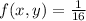 for
for
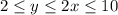
Now the distribution of x is given as
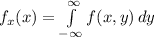
Here the limits for y are
 So the equation becomes
So the equation becomes
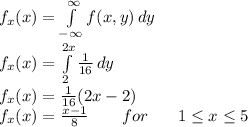
Part 2:
The probability is given as
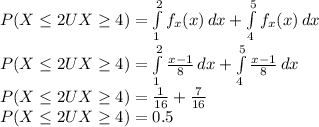
So the probability of X≤2 or X≥4 is 0.5.
Part 3:
The distribution of y is given as
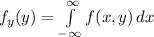
Here the limits for x are
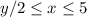 So the equation becomes
So the equation becomes
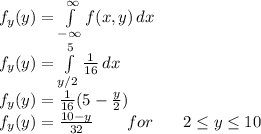
So the value of marginal probability of y is
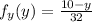 for
for
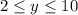
Part 4
The value is given as
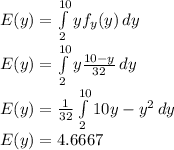
So the value of E(y) is 4.6667.
Part 5
This is given as
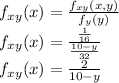
So the value of
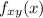 is
is
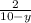 for
for
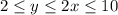
Part 6
The value is given as
![\geq M_(x,y)(y)=E(f_(xy)(x))=\int\limits^5_(y/2) {x f_(xy)(x)} \, dx \\M_(x,y)(y)=\int\limits^5_(y/2) {x (2)/(10-y)} \, dx \\M_(x,y)(y)=(2)/(10-y)\left[(x^2)/(2)\right]^5_{(y)/(2)}\\M_(x,y)(y)=(2)/(10-y)\left((25)/(2)-(y^2)/(8)\right)\\M_(x,y)(y)=(y+10)/(4)](https://img.qammunity.org/2021/formulas/mathematics/college/x7sf8qyofu7mi3dqex0dflqh6d6v5oldle.png)
So the value of
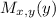 is
is

Part 7
The value is given as
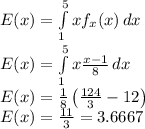
So the value of E(x) is 3.6667.
Part 8
The value is given as
![E(x,y)=\int\limits^(5)_1 \int\limits^(10)_2 {xyf_(x,y)(x,y)} \,dy\, dx\\E(x,y)=\int\limits^(5)_1 \int\limits^(10)_2 {xy(1)/(16)} \,dy\, dx\\E(x,y)=\int\limits^(5)_1 (x)/(16)\left[(y^2)/(2)\right]^(10)_2\, dx\\E(x,y)=\int\limits^(5)_1 3x\, dx\\\\E(x,y)=3\left[(x^2)/(2)\right]^5_1\\E(x,y)=36](https://img.qammunity.org/2021/formulas/mathematics/college/znooru5y8t7ces67ango9gp7j7fybbqxth.png)
So the value of E(x,y) is 36
Part 9
The value is given as
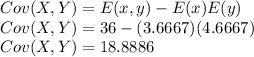
So the value of Cov(x,y) is 18.8886
Part 10
The variables X and Y are considered independent when
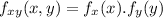
Here
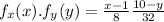
And
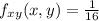
As these two values are not equal, this indicates that X and Y are not independent variables.