Question

Suppose that a drug test for an illegal drug is such that it is 98% accurate in the case of a

user of that drug (e.g. it produces a positive result with probability .98 in the case that the tested
individual uses the drug) and 90% accurate in the case of a non-user of the drig (e.g. it is negative
with probability .9 in the case the person does not use the drug). Suppose it is known that 10% of
the entire population uses this drug.
You test someone and the test is positive. What is the probability that the tested individual
uses this illegal drug?
What is the probability of a false positive with this test (e.g. the probability of obtaining a positive drug test given the person tested is a non-user)?
What is the probability of obtaining a false neg

Answer 1

(a) The probability that the tested individual uses this illegal drug given that the result is positive is 0.5213.

(b) The probability of a false positive is 0.10.

(c) The probability of a false negative is 0.02.

Explanation:

Let the events be denoted as follows:

D = an individual uses the illegal drug

X = the drug test result is positive.

The information provided is:

`P(X|D) = 0.98\\P(X^(c)|D^(c))=0.90\\P(D)=0.10`

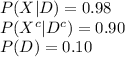
(a)

Compute the probability that the tested individual uses this illegal drug given that the result is positive as follows:

`P(D|X)=(P(X|D)P(D))/(P(X))`

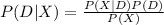
Compute the probability of the test result being positive as follows:

`P(X)=P(X|D)P(D)+P(X|D^(c))P(D^(c))\\=P(X|D)P(D)+[1-P(X^(c)|D^(c))][1-P(D)]\\=(0.98*0.10)+[(1-0.90)(1-0.10)]\\=0.188`

The probability that the tested individual uses this illegal drug given that the result is positive is:

`P(D|X)=(P(X|D)P(D))/(P(X))=(0.98*0.10)/(0.188) =0.5213`

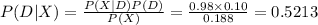
Thus, the probability that the tested individual uses this illegal drug given that the result is positive is 0.5213.

(b)

Compute the probability of a false positive given that the result was positive as follows:

`P(X|D^(c))=1-P(X^(c)|D^(c))=1-0.90=0.10`

Thus, the probability of a false positive is 0.10.

(c)

Compute the probability of a false negative as follows:

`P(X^(c)|D)=1-P(X|D)=1-0.98=0.02`

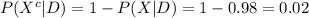
Thus, the probability of a false negative is 0.02.