Answer:
(a) The probability that the tested individual uses this illegal drug given that the result is positive is 0.5213.
(b) The probability of a false positive is 0.10.
(c) The probability of a false negative is 0.02.
Explanation:
Let the events be denoted as follows:
D = an individual uses the illegal drug
X = the drug test result is positive.
The information provided is:
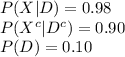
(a)
Compute the probability that the tested individual uses this illegal drug given that the result is positive as follows:
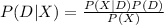
Compute the probability of the test result being positive as follows:
![P(X)=P(X|D)P(D)+P(X|D^(c))P(D^(c))\\=P(X|D)P(D)+[1-P(X^(c)|D^(c))][1-P(D)]\\=(0.98*0.10)+[(1-0.90)(1-0.10)]\\=0.188](https://img.qammunity.org/2021/formulas/mathematics/college/sh4whqood46686phkqiirs9xgcefn6kodg.png)
The probability that the tested individual uses this illegal drug given that the result is positive is:
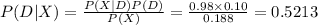
Thus, the probability that the tested individual uses this illegal drug given that the result is positive is 0.5213.
(b)
Compute the probability of a false positive given that the result was positive as follows:
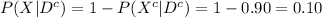
Thus, the probability of a false positive is 0.10.
(c)
Compute the probability of a false negative as follows:
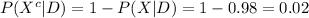
Thus, the probability of a false negative is 0.02.