Answer:
Transmissivity is

Step-by-step explanation:
So the well 1 has
r1=26ft
h1=29.34ft
The well 2 has
r2=73 ft
h2=32.56 ft
Converting the rate of flow from gal/min to ft3/day
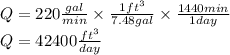
Now the transmissivity is is given as

Now by substituting values
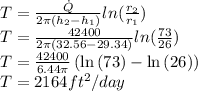
Now converting it to ft^2/sec
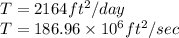
Transmissivity is
