Question

Prove that there are infinitely many primes of the form 3n+ 2 for a positive integern. [This is§4.1Problem 1, which comes with hint you might choose to use. You do not read to read beyond thefirst paragraph of§4.1.]

Answer 1

Proof with contradiction

Explanation:

Suppose there only finite odd prime numbers of the form 3n+2, and we call them
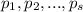`p_1,p_2,...,p_s`. Consider the number
`N=3p_1...p_n+2`. We can see that
`N\\ot =p_i$, for every [tex] t\in\{1,2,...,s\}`.

N is a odd number greater than 1, so it is a product of prime numbrs. We easily can see that N can be the product only of prime nubmbers of the form 3n+1 (because production of numbers od the form of 3n+1 is also number of the form 3n+1, and N is not of that form). So some prime number p of the form 3k+2 must divide N. We know that p can't be any prime number of the
`p_1,..,p_s`. Finally we have that p is also a prime number and it isn't
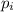`p_i` for any i less or equal to s. So the set of prime numbers of the form 3n+1 can't be finite.

We speak only of primes numbers of form 3n+1 and 3n+2, becaus numbers of the form 3n are not the prime number but 3. And forms for example 3n+4 is 3n+3+1=3(n+1)+1=3k+1. So we have just those two forms if we multiple n with 3.