Step-by-step explanation:
The given data is as follows.
Distance (s) = 20 m
time (t) = 0.775 s
Also, it is given that mass per 1 meter length (m) = 0.300 kg
Formula to calculate the velocity is as follows.
Velocity (v) =
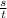
Putting the given values into the above formula as follows.
v =
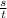
=
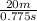
= 25.80 m/s
We know that,
v =
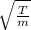
Taking square on both the sides, the formula will become as follows.
T =
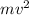
=
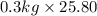
= 199.692 N
Therefore, we can conclude that tension in the given tightrope is equal to 199.692 N .