Answer:
Step-by-step explanation:
A = 3m
B = 4 m
let the angle between the two vectors is θ.
the resultant of two vectors is given by
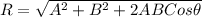
(a) R = 7 m
So,
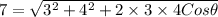
49 = 9 + 16 + 24 Cosθ
Cosθ = 1
θ = 0°
Thus, the two vectors are inclined at 0°.
(b) R = 1 m
So,

1 = 9 + 16 + 24 Cosθ
Cosθ = - 1
θ = 180°
Thus, the two vectors are inclined at 180°.
(c) R = 5 m
So,
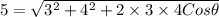
25 = 9 + 16 + 24 Cosθ
Cosθ = 0
θ = 90°
Thus, the two vectors are inclined at 90°.