Question

A 6.00 V lantern battery is connected to a 10.7 12 lightbulb, and the resulting current in the circuit is 0.323 A. You may want to review (Pages 602 - 606). Part A For related problem-solving tips and strategies, you may want to view a Video Tutor Solution of A dim flashlight. What is the internal resistance of the battery?

Express your answer to two significant figures and include the appropriate units. RinternalRinternal = nothingnothing SubmitRequest Answer Provide Feedback Next

Answer 1

7.9 Ω

Step-by-step explanation:

• Assuming that the lightbulb is in the linear region of operation, we can apply Ohm's law:

`V = I*R_(Tot)`

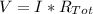
where V= 6.00 V, and I = 0.323 A

• We can solve for Rtot, as follows:

`R_(Tot) = (V)/(I) =(6.00V)/(0.323A) = 18.58 \Omega`

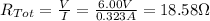
• This resistance, is equal to the sum of the resistance of the lightbulb, and the internal resistance of the battery, due both are connected in series (due to the current is the same at any point of the circuit):

`R_(Tot) = r_(int) +r_(lb) = 18.58\Omega`

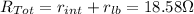
• Assuming that rlb = 10.7 Ω, we can find the internal resistance of the battery, just taking the difference between Rtot and Rlb:

`r_(int) = R_(Tot) - r_(lb) = 18.58 \Omega -10.7\Omega = 7.9 \Omega`

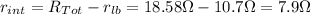
• The internal resistance of the battery is 7.9 Ω.